Alternating Currents in Phasor Diagrams

Showing alternating currents in phasor diagrams simplifies the calculation of networks with coils and capacitors. Such phasor diagrams use complex number notation to represent sine functions by peak amount and phase.

Followed by a short mathematical definition of complex numbers, I explain the mapping of cosine functions in complex pointer diagrams. As a specific example, current and voltage of an ideal coil are then compared in a phasor diagram and over time.

Complex Numbers

Complex numbers have real and imaginary parts forming the axes of the complex number plane.

Z = a + i * b
with i2 = -1

Z: complex number
a: real part
b: imaginary part
i: imaginary unit

In complex notation, the imaginary part is an ordinary or real number that is multiplied by the imaginary unit i2 = -1. Since there is no real number that produces a negative sign when multiplied by itself, the imaginary part of a complex number is outside the set of real numbers.

Alternating Currents by Amount and Phase

Complex numbers simplify the representation of alternating currents in amount and phase. For instance, in order to project a cosine signal

U = Up * cos(φ)

into the complex number plane, the cosine term is extended with an imaginary sine term i * sin(φ):

U = Up * ( cos(φ) + i * sin(φ) )

Up: peak amount of U
cos(φ) + i * sin(φ): complex phase term of U

Since real and imaginary axes of a complex coordinate system are orthogonal, the Pythagorean theorem applies to the phase term. Therefore, the sum of squares of sine and cosine terms equals the square of the amount of the phase term:

|cos(φ) + i * sin(φ)| = cos2(φ) + sin2(φ) = 1

The phase term therefore always has an amount of one, which is why a cosine signal with peak value Up turns into a rotating pointer with constant length Up in the complex number plane.

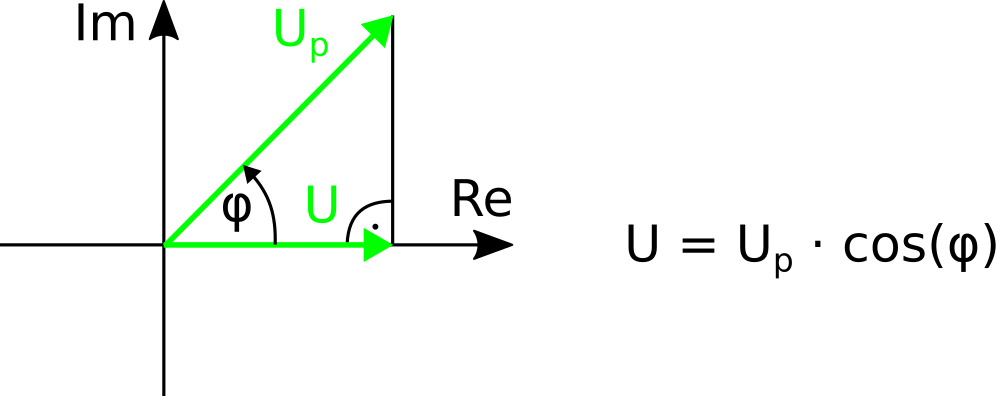
As shown in figure 1, the projection of the complex vector on the real axis preserves the original signal. For example, the pointer U at a phase angle φ = 0 has the same length as Up, while it disappears at φ = 90°. However, since the length of the pointer Up remains constant, there is no need to work with sine and cosine signals in the complex number plane.

Most of the time, mathematical treatises use the exponential function with imaginary exponent instead of splitting the phase term into sine and cosine parts.

cos(φ) + i * sin(φ) = eiφ
U = Up * eiφ

Example: Voltage and Current in an Ideal Coil

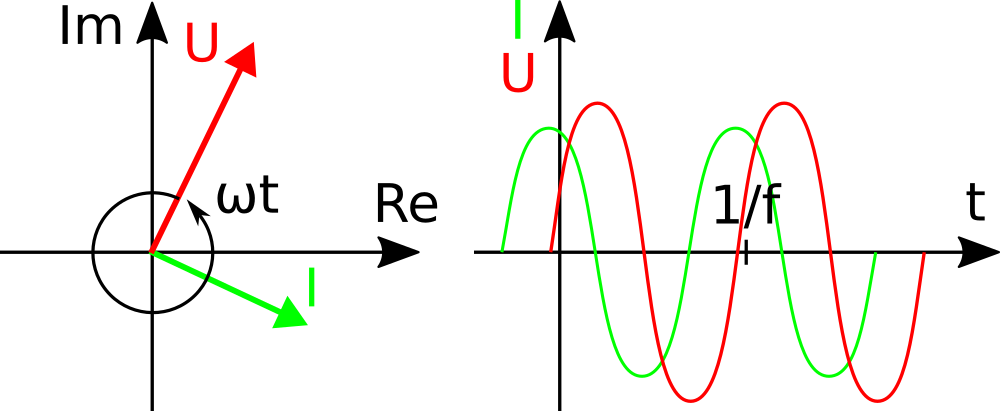
Figure 2 shows voltage and current of an ideal coil with pointers in the complex number plane on the left and signals in the course of time on the right. Pointers for current I and voltage U rotate counter-clockwise with speed ω around the intersection of the imaginary and real axes of the complex number plane. On the right we see the sine curves from the projection of the pointer on the real axis.

With ω = 2πf a complete rotation of 2π or 360° is made at time 1/f, f being the frequency of signals in Hertz. On the left, pointers return to their original locations after full turns, while the cycles of the sine curves repeat themselves at the marker for t = 1/f. At any time, the real voltages and currents are the projections of the complex pointers onto the real number axis.

One great advantage of the use of complex numbers is to simply add vectors instead of working with sine and cosine signals. To see an example of this use of phasor diagrams, you could read the article on measuring impedances.

References

Pythagorean theorem: Wikipedia.org

Complex numbers: Wikipedia.org

Phasor diagram: Wikipedia.org

Related Topics

Alternating currents as complex numbers in German: mantelwelle.de